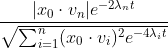Following this question:

where v_i are eigenvectors of GOE and x_0 is the initial vector generated in the above code.

Based on the answer, my code is as follows:

h1t <- function(t) {
  h10 <- c(x_0 %*% v[, n])
  numer <- abs(h10) * exp(-2*l[n] * t)
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*l * .t))
  }, numeric(1L))
  numer/sqrt(denom)
}


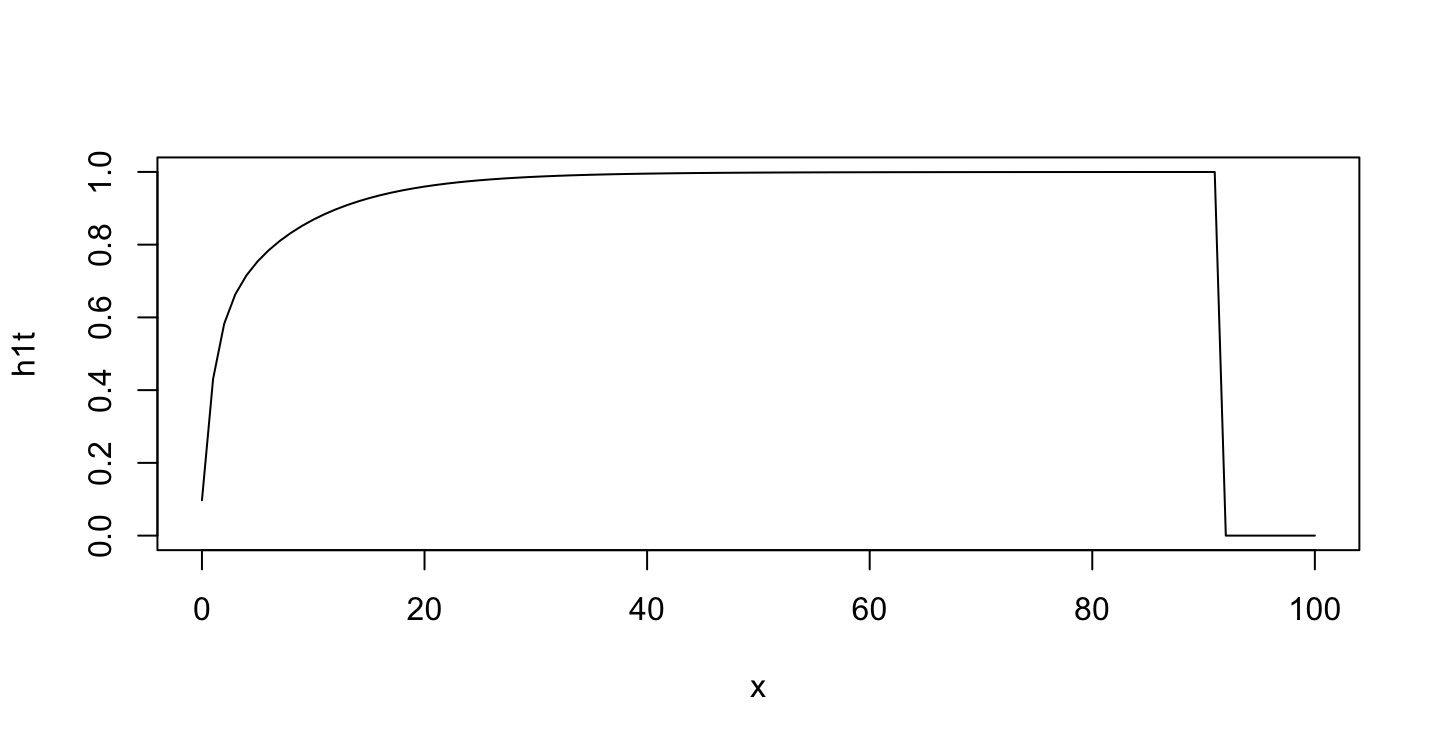
plot(h1t, from = 0, to = 100)

However, after t=80, there would be NaN in the function.

> h1t(90)
[1] 0.9997982
> h1t(100)
[1] 0
> h1t(400)
[1] NaN

The plot:

How to fix this problem?

CodePudding user response：

h_10 in your function is a 1x1 matrix, and this is the source of the warning. You can coerce it to a single number with c, or by extracting its [1, 1]-entry.

The more serious problem is here:

sum((x_0 %*% v)^2 * exp(-4*l * t))

If t is a single number, there's no problem. But if it is a vector, this expression is mixing some vectors having different length. You have to map the vector t, with sapply or vapply for example:

h1t_modefied <- function(t) {
  h10 <- c(x_0 %*% v[, n])
  numer <- abs(h10) * exp(-2*l[n] * t)
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*l * .t))
  }, numeric(1L))
  numer/sqrt(denom)
}

By the way I don't see the ^2 in your formula in the picture.

> h1t_modefied(1:2)
[1] 0.5734668 0.7033437
> h1t_modefied(1)
[1] 0.5734668

If you want to use curve you have to use x for the variable, not t:

curve(h1t_modefied(x), from = 0, to = 20)

EDIT

You updated your question, asking why the function is vanishing for large t. This is because the exponentials in the sum at the denominator are huge numbers and this sum becomes infinite.

You can improve your function to avoid these huge numbers:

# original function

h1t_A <- function(t) {
  h10 <- c(x_0 %*% v[, n])
  numer <- abs(h10) * exp(-2*l[n] * t)
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*l * .t))
  }, numeric(1L))
  numer/sqrt(denom)
}

# improved function
h1t_B <- function(t) {
  h10 <- c(x_0 %*% v[, n])
  denom <- vapply(t, function(.t) {
    sum((x_0 %*% v)^2 * exp(-4*(l - l[n]) * .t))
  }, numeric(1L))
  abs(h10) / sqrt(denom)
}

# > h1t_A(10)
# [1] 0.8847206
# > h1t_B(10)
# [1] 0.8847206
# > h1t_A(100)
# [1] 0
# > h1t_B(100)
# [1] 0.9949121
# > h1t_B(400)
# [1] 0.9999991

The idea is to divide the numerator and the denominator by the exponential term of the numerator.