I would like to generate a random truncated normal distribution with the following properties.

1. lower bound= 3
2. higher bond= 5
3. using a fixed set of values at the first digit(3.0,3.1,3.2,...,4.9,5.0)
4. With mode=3
5. the probability of 5 occurring should be 50% of the probability of 3 occurring.

I was able to deal with the first 3 steps but I am struggling to find a way to set mode=3 and to establish a fixed relationship on the occurrence of the higher and lower bound.

library(truncnorm)
library(ggplot2)
set.seed(123)
dist<- as.data.frame(list(truncnorm=round(rtruncnorm(10000, a=3, b=5, mean=3.3, sd=1),1)))
ggplot(dist,aes(x=truncnorm)) 
  geom_histogram(bins = 40) 
  theme_bw()

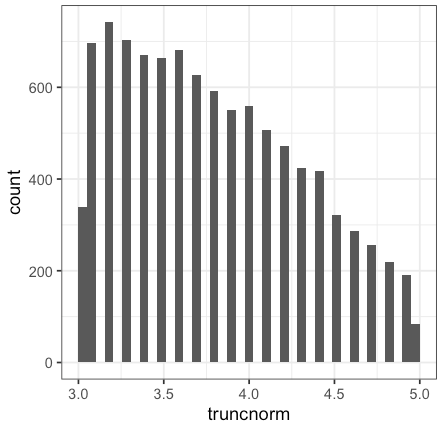
As you can see I can create truncated normal with the desired boundaries. The problem with this distribution are two.

• First I want truncnorm==3.0 to be the mode (i.e. most frequent value of my distribution, while in this case the mode is truncnorm==3.2
• Second I want the count of 5.0 values to be 50% of the 3.0 values. For example, if I generated a distribution with 800 observations with truncnorm=3.0, there should be approximately 400 observations with truncnorm=5.0.

CodePudding user response：

Luckily, all your requirements are achievable using a truncated normal distribution.

Let low = 3 and high = 5.

Simply evaluate the density (at discrete points such as 3.0, 3.1, ..., 4.9, 5.0) of a normal distribution with mean low and standard deviation sqrt(2)*(high-low)/(2*sqrt(ln(2)).

This standard deviation is found by taking the following function proportional to a normal density with mean 0 and standard deviation z:

 f(x) = exp(-(x-0)**2/(2*z**2))

Since f(0) = 1, we must find the necessary standard deviation z such that f(x) = 1/2. The solution is:

 g(x) = sqrt(2)*x/(2*sqrt(ln(2))

And plugging high-low into x leads to the final standard deviation given above.