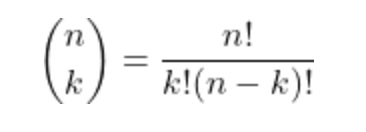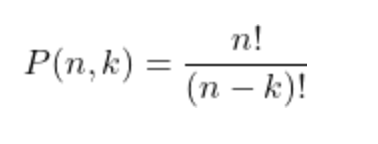swift - (n C k) and (n P k) - built in function for combinations and permutations?-CodePudding

What is the built in way to do these in Swift? Or with an official Apple library?

(n C k)

python3.8: math.comb(n,k)

(n P k)

python3.8: math.perm(n,k)

CodePudding user response：

Swift does not provide built-in functions for permutation, combination, or even factorial. But these simple formulas are easy to implement.

Here is a trivial factorial function:

func factorial(_ n: Int) -> Int {
    return (1...n).reduce(1, { $0 * $1 })
}

But note that this will crash where n >= 21 since 21! is too large to fit in an Int variable.

Here is a naive implementation of "perm":

func perm(n: Int, k: Int) -> Int {
    return factorial(n) / factorial(n - k)
}

And for "comb" you can do:

func comb(n: Int, k: Int) -> Int {
    return perm(n: n, k: k) / factorial(k)
}

However, there is a simple improvement to be made for "perm". Let's say n = 5 and k = 2. You can write the formula for perm as:

n!     = 5!     = 5! = 1 * 2 * 3 * 4 * 5
------   ------   --   -----------------  = 4 * 5
(n-k)! = (5-2)! = 3! = 1 * 2 * 3

This boils down to "perm" being equal to (n-k 1) * (n-k 2) * ... n

So let's rewrite the functions to be more efficient:

func mult(_ range: ClosedRange<Int>) -> Int {
    return range.reduce(1, { $0 * $1 })
}

func perm(n: Int, k: Int) -> Int {
    return mult((n - k   1)...n)
}

func comb(n : Int, k: Int) -> Int {
    return perm(n: n, k: k) / mult(1...k)
}

Note that the "comb" function didn't actually change other than to use mult(1...k) instead of factorial(k) which both give the same result.

These functions still have limits on the sizes of n and k before they will crash due to the limits on the Int data type.