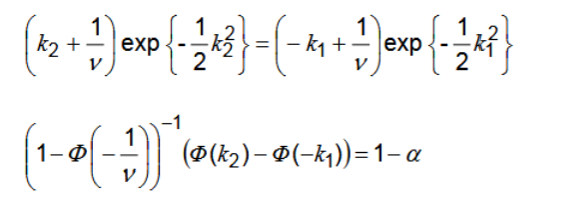Iterative solving of 2 equations results in "cannot determine truth value of Relational"-CodePudding

I am given these 2 equations with given values for a (alpha) and v. I know that these cannot be solved classically but iteratively, so I want to use sympy and scipy to calculate phi (distribution).

My main goal is to calculate k1 and k2 (substituted with x and y in the code).

(I substitute k1 with x and k2 with y, alpha with a.)

from sympy import symbols, Eq, solve, exp
from scipy.stats import norm

x, y = symbols('x y')
v = 2.2526  # given
a = 0.1  # given

eq1 = (x   (1/v)) * exp((-(1/2)) * (x**2)) - (-y   (1/v)) * exp((-(1/2)) * (y**2))
eq2 = (((1 - norm.cdf(-1/v))**-1) * (norm.cdf(y) - norm.cdf(-x))   a - 1)

sol = solve((eq1, eq2), (x, y))
print(sol)

If I run this I get

TypeError("cannot determine truth value of Relational")

What does this error mean?

Edit1:

x, y = symbols('x y', real=True)

leads to

TypeError: ufunc 'isnan' not supported for the input types, and the inputs could not be safely coerced to any supported types according to the casting rule ''safe''

CodePudding user response：

Using your code and the hint provided by this comment, the following code can provide a numerical solution:

from sympy import symbols, exp, nsolve, solve
from sympy.stats import Normal, cdf

x, y = symbols('x y')
T = Normal("t", 0, 1)
v = 2.2526  # given
a = 0.1  # given

eq1 = (x   (1 / v)) * exp((-(1 / 2)) * (x ** 2)) - (-y   (1 / v)) * exp((-(1 / 2)) * (y ** 2))
eq2 = (((1 - cdf(T)(-1 / v)) ** -1) * (cdf(T)(y) - cdf(T)(-x))   a - 1)

sol = nsolve((eq1, eq2), (x, y), (1, 1))
# sol = solve((eq1, eq2), (x, y), (1, 1))
print(sol)

# output is: Matrix([[2.42082817559350], [0.284669014405097]])

The normally distributed continuous random variable with mean 0 and variance 1 is specified by T = Normal("t", 0, 1), and the CDF is specified as cdf(T). nsolve requires the caller to provide an estimate of the answer as for a starting point, so I guessed (1,1) and it worked.

CodePudding user response：

Google found this.

This first answer suggests something to try:

The problem is that the solver needs to know the sign of a certain expression in terms of the coefficients (the discriminant of a polynomial), and it cannot determine the sign based on the information given, as the discriminant ends up being D = (1/(c2*r2) - 1/(c1*r1))**2. Symbols are not automatically assumed real; so the square of some expression like that could even be negative. It's a good idea to declare symbols as real, by

python sym.symbols('i, r1, c1, r2, c2, t', real=True)

but this doesn't solve the problem because it might happen that c1*r1 == c2*r2, and then D is 0.

CodePudding user response：

The missing error message:

In [13]: from scipy.stats import norm

In [14]: eq2 = (((1 - norm.cdf(-1/v))**-1) * (norm.cdf(y) - norm.cdf(-x))   a - 1)
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Input In [14], in <cell line: 1>()
----> 1 eq2 = (((1 - norm.cdf(-1/v))**-1) * (norm.cdf(y) - norm.cdf(-x))   a - 1)

File ~\anaconda3\lib\site-packages\scipy\stats\_distn_infrastructure.py:1955, in rv_continuous.cdf(self, x, *args, **kwds)
   1953 x = np.asarray((x - loc)/scale, dtype=dtyp)
   1954 cond0 = self._argcheck(*args) & (scale > 0)
-> 1955 cond1 = self._open_support_mask(x, *args) & (scale > 0)
   1956 cond2 = (x >= np.asarray(_b)) & cond0
   1957 cond = cond0 & cond1

File ~\anaconda3\lib\site-packages\scipy\stats\_distn_infrastructure.py:1000, in rv_generic._open_support_mask(self, x, *args)
    998 a, b = self._get_support(*args)
    999 with np.errstate(invalid='ignore'):
-> 1000     return (a < x) & (x < b)

File ~\anaconda3\lib\site-packages\sympy\core\relational.py:511, in Relational.__bool__(self)
    510 def __bool__(self):
--> 511     raise TypeError("cannot determine truth value of Relational")

TypeError: cannot determine truth value of Relational

Or using the norm by itself:

In [16]: norm.cdf(y)
---------------------------------------------------------------------------
...
TypeError: cannot determine truth value of Relational

It's trying to test whether the argument x is within a certain range. If x is a symbol that isn't a simple yes/no case.

Or narrowing it down even further, a symbolic relational, like y<2 cannot be used in a context that expects a simple python True/False value. With arrays we often see a ambiguity error; this is a symbolic equivalent:

In [22]: bool(y<2)
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
Input In [22], in <cell line: 1>()
----> 1 bool(y<2)

File ~\anaconda3\lib\site-packages\sympy\core\relational.py:511, in Relational.__bool__(self)
    510 def __bool__(self):
--> 511     raise TypeError("cannot determine truth value of Relational")

TypeError: cannot determine truth value of Relational

In general, using sympy expressions and symbols in numpy and scipy does not work. For limited cases involving addition and multiplication it's ok, but beyond that you'll like get errors. Use sympy's own functions instead.