AttributeError: 'tuple' object has no attribute 'ndim' matplotlib-CodePudding

I am trying to generate a plot for double integral using python, matplotlib. X and Y ranges are defined and Z is the double integral of X and Y.

import matplotlib.pyplot as plt
import numpy as np
import scipy
from scipy.integrate import dblquad

fig, ax = plt.subplots(subplot_kw={"projection": "3d"})

def function_I(x, y):
    return np.sin(x)*np.cos(y/5)

#Make data
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
Z = scipy.integrate.dblquad(function_I, -5, 5, -5, 5)

# plot the surface
ax.plot_surface(X, Y, Z)

fig.colorbar(surf, shrink=0.5, aspect=5)

plt.show()

line

ax.plot_surface(X, Y, Z)

gives

AttributeError: 'tuple' object has no attribute 'ndim'

some similar question provided solutions related to .shape and .reshape? Doesn't make a whole lot sense. Any comments appreciated!

CodePudding user response：

dblquad(function_I, -5, 5, -5, 5) calculates the integral of one complete area, so resulting in a single value.

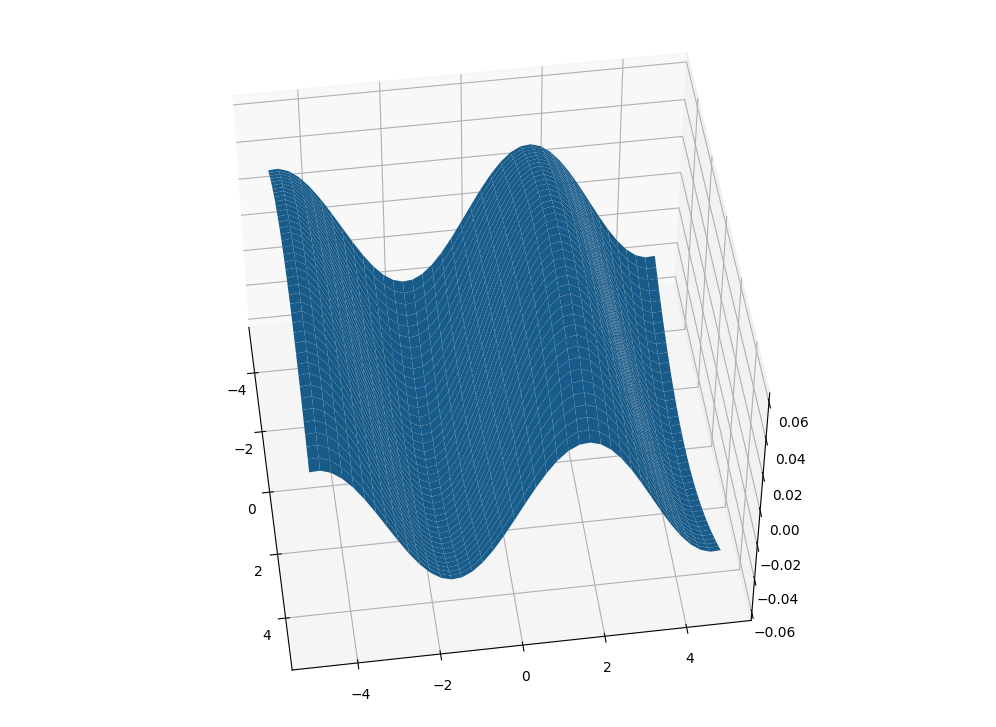
The following approach intents to calculate the integral for each little patch between successive coordinates. And then draw a surface using the mean XY position of each patch.

import matplotlib.pyplot as plt
import numpy as np
from scipy.integrate import dblquad

def function_I(x, y):
    return np.sin(x) * np.cos(y / 5)

# Make data
X = np.linspace(-5, 5, 41)
Y = np.linspace(-5, 5, 41)
X, Y = np.meshgrid(X, Y)
Z = np.zeros_like(X)
for i in range(1, X.shape[0]):
    for j in range(1, X.shape[1]):
        Z[i, j], _ = dblquad(function_I, X[i - 1, j - 1], X[i, j], Y[i - 1, j - 1], Y[i, j])

# plot the surface
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.plot_surface((X[:-1, :-1]   X[1:, 1:]) / 2, (Y[:-1, :-1]   Y[1:, 1:]) / 2, Z[1:, 1:])

plt.show()